Problemlösning och språkutveckling i matematik

Mitt namn är Sandra Straumits och jag arbetar som lärare i matematik och svenska på Allvar Gullstrandgymnasiet i Landskrona. På olika sätt har jag genom åren försökt utveckla min undervisning, så att den ska bli intressant och lärorik för eleverna. Fokus har till största delen legat på matematikämnet, då många av de elever jag träffar har svårt och dåligt självförtroende när det gäller ämnet. Något som har fungerat bra i mina klasser är när jag arbetar med undersökande aktiviteter, problemlösning och laborationer i matematik. Laborationer kan innebära att eleverna får undersöka matematiska samband konkret med händerna eller med hjälp av datorn. På senare tid har jag också börjat intressera mig för hur man kan arbeta mer språkutvecklande i ämnet.

Språkutvecklande arbetssätt

Vad innebär det då att arbeta språkutvecklande i ett ämne? I artikeln ”Språkutvecklande arbetssätt i matematik” nämner Maike Hajer, Björn Kindenberg och Sara Ramsfeldt tre stycken grundprinciper för språkutvecklande undervisning. Den första innebär att koppla matematiken till vardagliga situationer som eleverna kan relatera till. Att man utgår från något konkret för att komma till något mer abstrakt. Den andra grundprincipen innebär att eleverna ska kommunicera matematik både muntligt och skriftligt genom att interagera med varandra och med läraren. Här kan problemlösning i grupp vara ett sätt att arbeta med detta. Den sista principen innebär att man som lärare måste ge eleverna språklig stöttning, så att de kan utvecklas och bli självständiga i sitt matematiska språkanvändande. Språklig stöttning kan till exempel innebära att en elev förklarar hur den löst en uppgift med ett vardagligt språk och läraren förstärker/sammanfattar förklaringen med korrekta matematiska begrepp. Det är viktigt att skapa en struktur för konstruktiva samtal, det vill säga en klassrumskultur där man är respektfull mot varandra och där det finns ett tillåtande klimat, så att eleverna vågar redovisa och diskutera sina och kamraternas lösningar.

Klassrumsexempel 1

Mitt första klassrumsexempel har jag utvecklat från en lektion jag genomfört tidigare där syftet var att eleverna skulle arbeta med problemlösnings- och modelleringsförmågan och försökt göra den lektionen mer språkutvecklande.

Bakgrunden till lektionen är att vi i kursen Matematik 2b har arbetat med hur man med hjälp av en graf kan bestämma den räta linjens ekvation på formen 𝑦=𝑘𝑥+𝑚. Lektionen i fråga ska eleverna lära sig hur man kan bestämma den räta linjens ekvation algebraiskt om man har två punkter på linjen givna. Detta innefattar att kunna arbeta med en formel för att bestämma linjens lutning, samt genom att sätta in värden för x, y och k i den räta linjens ekvation, kunna lösa ut variabeln m. Jag ville att eleverna själva skulle hitta strategier för att kunna göra detta genom att arbeta med följande problemformulering:

”Pelle och Måns ska handla äpplen på torget. De köper samma sort. Pelle köper 5,2 kg och får betala 32,68 kr, medan Måns får betala 16.75 kr för 2,5 kg. I respektive pris ingår också kostnaden för en påse. Ta reda på äpplenas kilopris, vad en påse kostar samt teckna en formel som man kan använda för att beräkna totalkostnaden för ett inköp.”

Uppgiften kan tyckas, med den erfarnes ögon, väldigt elementär, men blir just denna lektion ett problem, då eleverna i stunden inte har lärt sig metoden ännu. De har sedan tidigare kunskap om metoder för att bestämma k- och m-värdet med hjälp av en graf, men har då utgått från punkter med heltalskoordinater. Lösningen av problemet innebär att de dels ska inse att respektive mängd äpplen och kostnader matematiskt kan representeras som punkter i ett koordinatsystem, att k-värdet motsvarar kilopriset för äpplena och m-värdet representerar kostnaden för påsen. Sedan ska de försöka klura ut hur de ska hantera situationen när värdena de arbetar med inte är heltal längre, utan att koordinaterna har decimaler.

För att göra lektionen mer språkinriktad och att eleverna skulle ”tvingas” att samarbeta och tala matematik, valde jag att dela upp problemformuleringen på små kort, som jag laminerade (se bild nedan). Jag delade in eleverna i grupper om tre, så varje elev blev ansvarig för att delge gruppen informationen från tre kort. De uppmanades att inte visa de andra gruppmedlemmarna sina kort, utan informationen på korten skulle delges gruppen muntligt, men kunde upprepas hur många gånger som helst.

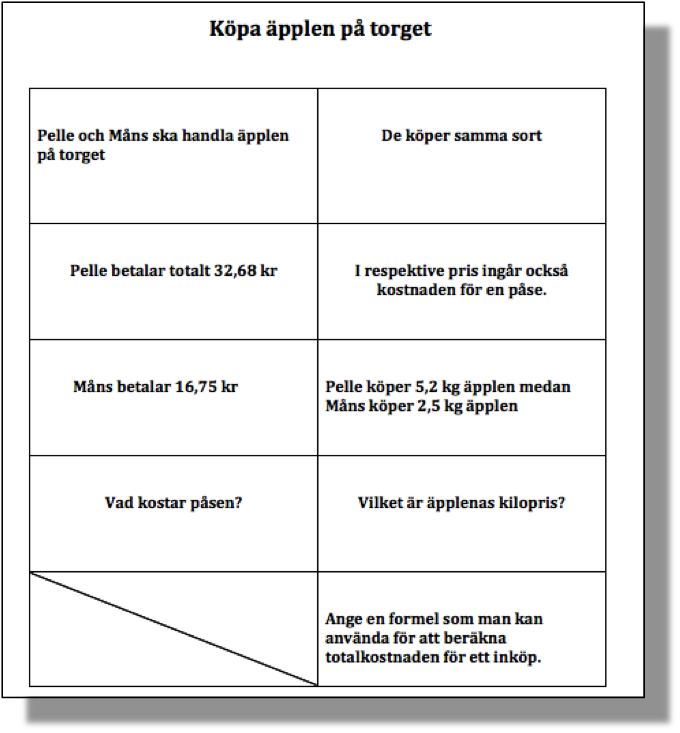
Detta fungerade ganska bra i grupperna. Det blev mycket matematikkommunikation, men med konsekvensen att svårighetsgraden i problemlösningen blev högre, eftersom eleverna hela tiden fick fråga varandra om information och de ställda frågorna i uppgiften behövde nödvändigtvis inte komma i samma ordning som i ursprungsformuleringen. Som vanligt blev det mycket intressant att gå runt och lyssna på elevernas diskussioner och problemlösningsstrategier. För mig som lärare fick jag ett ganska bra hum om vad eleverna inte kunde. Värdefull information inför den kommande lösningsdiskussionen och genomgången senare under lektionen där eleverna skulle bli introducerade för formeln:

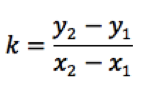
En del grupper fick jag hjälpa på traven genom att tipsa om vilken frågeformulering de skulle koncentrera sig på först och för andra grupper som fastnat totalt, hinta om att de kunde fundera på hur de kunde tillämpa det vi arbetat med tidigare lektioner.

Idén att dela upp problemformuleringen fick jag efter att ha läst Pauline Gibbons bok Lyft språket lyft tänkandet. Där skriver hon bland annat om hur man kan integrera språkliga aktiviteter med ämnesundervisningen. Hon skriver att det är viktigt att det i kommunikativa aktiviteter ska finnas ”informationsgap”. I det här fallet innebär det att alla i gruppen inte har tillgång till samma information, utan att man måste delge varandra denna för att kunna lösa problemet. Eleverna måste använda språket för att kunna lösa uppgiften. Detta ledde mina tankar till en gammal problemsamling jag bläddrat i för länge sedan, där problemformuleringarna just är uppdelade på kort och tanken är att man ska lösa problemen gemensamt i små grupper. Problemsamlingen som är skriven av Tim Erickson heter Gemensam problemlösning 1 och riktar sig till skolår 4 till 6, men konceptet kan man använda på vilket problem som helst. Är man nyfiken på materialet har Peter Sandin skrivit en artikel om det i tidskriften Nämnaren.

Grupperna fick 30 minuter på sig att försöka lösa problemet. Efter detta var det dags för nästa språkutvecklande aktivitet. Jag gick runt och fotograferade elevernas lösningar med min Ipad och efter det valde jag ut tre stycken lösningar som jag ville att vi skulle diskutera gemensamt i klassrummet. Jag projicerade upp bilden på lösningarna en i taget på SMART-boarden och så fick respektive grupp presentera sin lösning för klasskamraterna. När en grupp hade förklarat vad de gjort och kommit fram till fick klasskamraterna ställa frågor till gruppen om de ville få lösningen förtydligad, tala om vad som var bra med lösningen, samt vad som kunde göras bättre.

I detta moment försökte jag ge eleverna språklig stöttning genom att vid behov upprepa eller sammanfatta vad de sagt och vid behov tillföra de korrekta matematiska termerna. Denna övning blev också språkutvecklande genom att eleverna fick se exempel på lösningar av olika kvalité och att de fick höra och använda olika matematiska begrepp.

Den första lösningen som presenterades och diskuterades var denna:

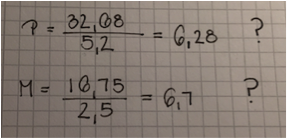
Den här gruppen fick följande feedback från sina klasskamrater:

• Lösningen kunde förtydligas genom att de kunde skrivit att det var kilopriset de försökt komma fram till.
• De hade kunnat skriva en förklaring till varför de satte frågetecken efter beräkningarna. Dock framgick det vid den muntliga redovisningen att gruppen insett att kilopriset måste bli samma i båda beräkningarna, men inte kommit vidare i sitt resonemang. Här fick de också förklaringen av sina kamrater att det är för att priset på påsen också ingår i totalbeloppet för de båda inköpen.

Anledningen till att jag valde just denna lösning är att jag ville belysa ett vanligt fel många elever gör, nämligen att de tolkar sambandet som en proportionalitet.

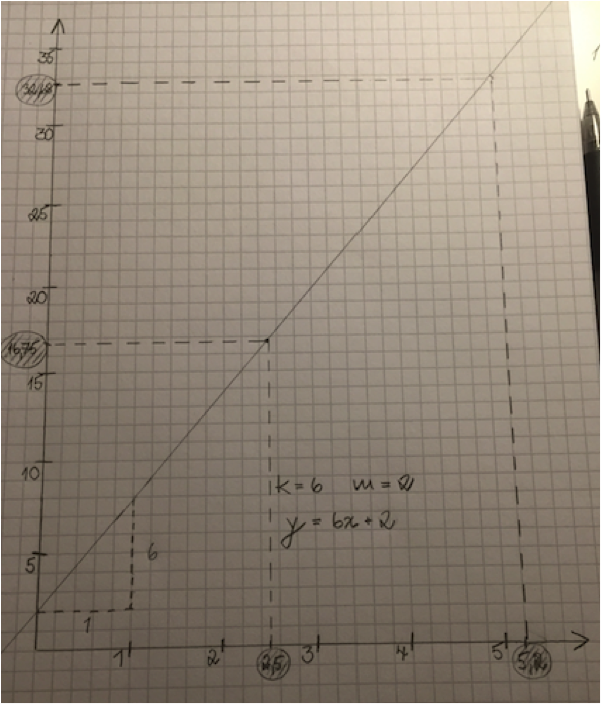
Nästa lösning som jag projicerade upp på SMART-boarden var denna:

Efter att gruppen redovisat sin lösning fick denna grupp följande feedback från klasskamraterna för att förbättra sin lösning:

• De hade kunnat förtydliga vad grafen visar genom att skriva ut att x-axeln representerar mängden äpplen och y-axeln representerar totalkostnaden.
• Vara noggrannare, då punkterna inte riktigt överensstämmer med den ritade linjen. Ingen av punkterna ligger riktigt på linjen.
• Skriva ut vad de har kommit fram till – vad symboliserar koefficienten 6 och konstanten 2 i den räta linjens ekvation som de tecknat ner?

Mitt syfte att lyfta fram denna grupps lösning, var att markera att en grafisk lösning inte alltid är lämplig om man ritar för hand. Detta eftersom punkternas koordinater har decimaler och blir därför svåra att pricka in exakt om man inte har ett datorprogram eller grafritande räknare till hjälp.

Den sista lösningen som redovisades och diskuterades var denna:

Denna grupp fick följande feedback för hur lösningen kunde förbättras:

• Att definiera sina variabler. Vad symboliserar x och y?
• Förtydliga att k-värdet är kilopriset och m-värdet kostnaden för påsen, även om detta framgick vid redovisningen.

Mitt syfte med att visa denna lösning för klassen var att eleverna skulle se att det ibland räcker med att rita en skiss över en graf. Här visar eleverna hur man kan räkna fram k-värdet (kilopriset) med hjälp av det samband de lärt sig sedan tidigare: att dividera differensen mellan koordinaterna i y-led med differensen mellan koordinaterna i x-led. Jag använde också denna grupps lösning som utgångspunkt i den genomgång jag gjorde efter lösningsdiskussionen, där formeln för att bestämma k-värdet och proceduren att lösa ut m-värdet algebraiskt presenterades för eleverna. Min förhoppning med problemlösningsuppgiften och lösningsdiskussionen var att eleverna skulle ha fått en förförståelse för situationen och skulle förstå abstraktionen bättre.

Efter genomgången fick eleverna möjlighet att utveckla sin procedurförmåga genom att arbeta med rutinuppgifter för att befästa metoden för att beräkna k-värdet och m-värdet algebraiskt.

Tidsåtgång för de olika momenten var 30 minuter problemlösning, 20 minuter redovisning och feedback, ca 15 minuter genomgång och 15 minuter arbete med rutinuppgifter. Lektionen varade 80 minuter.

Klassrumsexempel 2

Mitt andra klassrumsexempel genomförde jag några lektioner senare i samma klass. Denna lektion varade i 60 minuter. Syftet med denna lektion var att eleverna återigen skulle arbeta med problemlösningsförmågan och denna gång få en förförståelse för vad lösningen till ett ekvationssystem innebär. Även denna gång fick de arbeta i grupper om tre. Fördelen med grupparbete är att eleverna får stöttning av varandra i lösningsprocessen. Elever som inte hade lyckats på egen hand, klarar med hjälp av gruppen att lösa problemet. De elever som får förklara för den som inte riktigt förstår utmanas också och får möjlighet att utveckla sin begreppsbildning.

Problemet eleverna skulle arbeta med löd så här:

Det har gått en månad sedan Ichiros mamma lades in på sjukhuset. Han har bestämt sig för att be en bön med sin lillebror i templet varje morgon för att mamman snart ska bli bra. I Ichiros plånbok finns det 18 stycken tio-yen-mynt och i den yngre broderns plånbok finns 22 stycken fem-yen-mynt. De har bestämt sig för att varje gång ta ett mynt från var och en och stoppa i myntboxen. De ska fortsätta be tills endera plånboken är tom. Efter avslutad bön tittar de en dag i sina plånböcker och upptäcker att den yngre brodern har mer pengar kvar än Ichiro. Frågan är: Hur många dagar är det sedan de började be.

Efter att eleverna löst problemet skulle de försöka att redovisa sin lösning med så många olika representationer som möjligt i ett fyrfältsblad. Se bild nedan.

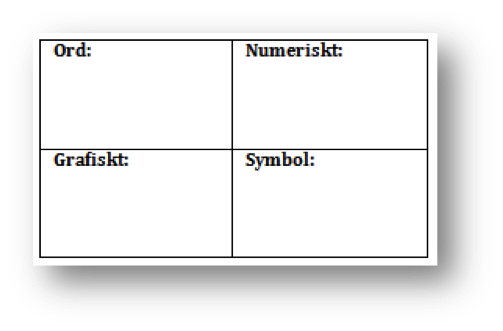
Elisabeth Rystedt och Lena Trygg skriver i sin bok Matematikverkstad följande formulering: ”Förmåga att uttrycka sig på flera sätt i matematik är ett tecken på god förståelse” (s. 63) Ovan beskrivna övning är ett sätt för eleverna att öva upp sin begreppsbildning, samtidigt som de övar sin kommunikativa förmåga. Enligt författarna är just begreppsutvecklingen ett utav de viktigaste målen för undervisningen i matematik.

De flesta grupperna löste först problemet numeriskt genom att ställa upp en tabell och systematiskt undersöka när lillebroderns summa översteg Ichiros. De allra flesta förenklade också problemet genom att de räknade med kronor i stället för yen. Efter att de löst uppgiften utmanades de i att försöka visa lösningen på problemet på olika sätt. Nedan är några exempel på de fyrfältsblad som eleverna lämnade in. Jag använde en kombination av deras lösningar nästkommande lektion för att introducera grafisk lösning av ekvationssystem och vad lösningen av ett ekvationssystem innebär.

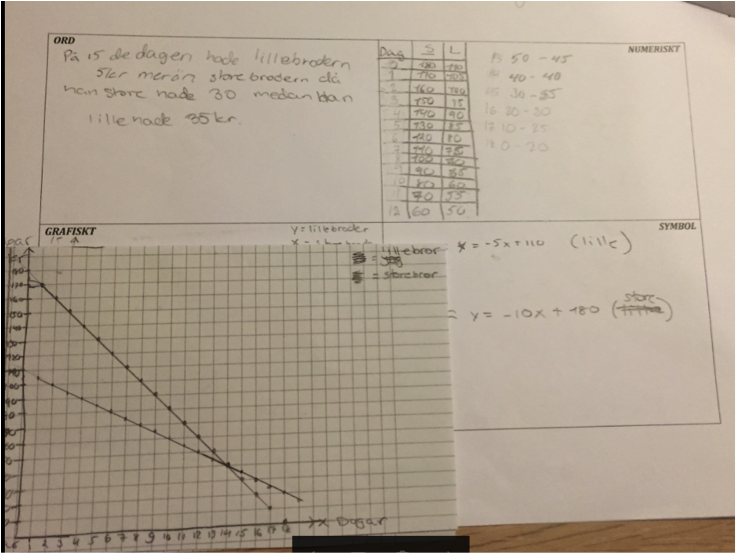
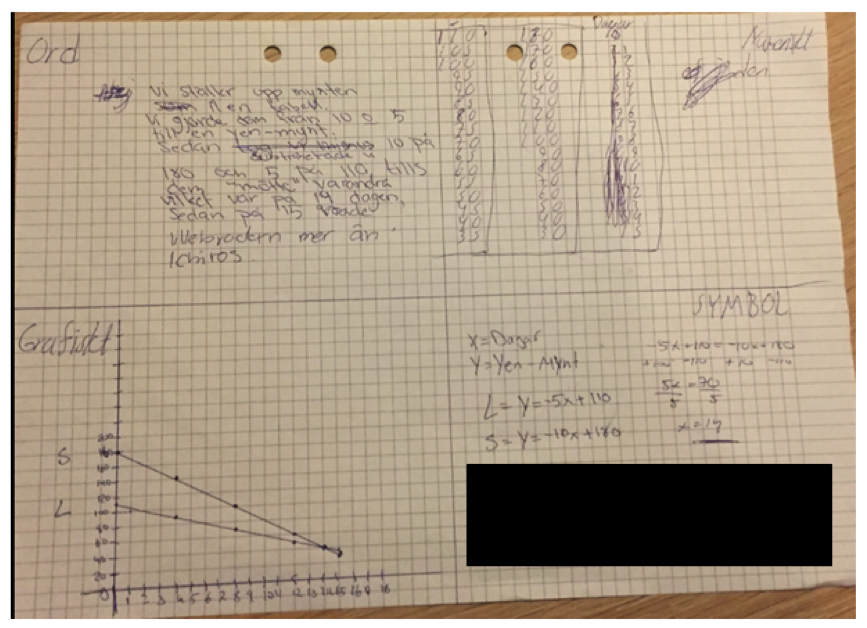
Att eleverna får arbeta undersökande – dvs att utgå från något bekant och upptäcka ”nya” samband själva är ett sätt för eleverna att lämna sin närmaste trygghetszon och ge sig in i den närmaste utvecklingszonen. Detta är begrepp som är hämtade från Vygotskijs sociokulturella syn på lärande och också något Pauline Gibbons understryker som viktigt i att skapa ett klassrum där elever får arbeta med uppgifter som kräver en hög kognitiv utmaning. Här är det viktigt att eleverna får stöttning för att klara uppgiften. I mina två klassrumsexempel har eleverna haft varandra och mig som lärare som stöttning i sin problemlösning, kommunikation och begreppsutveckling.

För den som är intresserad och vill fördjupa sig ytterligare i gemensam problemlösning och hur man kan arbeta språkutvecklande i sitt ämne finns lite tips på litteratur nedan.

Litteraturlista

Erickson, T. (1993) Gemensam problemlösning 1, Liber AB, Stockholm

Gibbons, P. (2013) Lyft språket lyft tänkandet – språk och lärande, Hallgren & Fallgren, Stockholm

Hajer, M. Kindenberg, B. Ramsfeldt S. (2015) Språkutvecklande arbetssätt i matematik.

Rydstedt E, Trygg L. (2005) Matematikverkstad, NCM: Göteborgs universitet

Sandin, P. (1991) Gemensam problemlösning, (Nämnaren 3: 4, 1991) http://ncm.gu.se/pdf/namnaren/116120_91_3-4.pdf