Konkretisering av decimaltal
Mitt namn är Maria Davidsson Friberg och jag arbetar på Västervångskolan i Landskrona. I grunden är jag ma/no-lärare för åk 1-7 men har vidareutbildat mig till speciallärare med inriktning mot matematikutveckling, jag är även förstelärare i matematik. I mitt uppdrag ger jag särskilt stöd åt elever, individanpassar material, handleder lärare och arbetar med ämnesutveckling och systematiskt kvalitetsarbete. I skrivande stund är jag och några kollegor till mig mitt uppe i ett spännande utvecklingsarbete kring elever med särskild begåvning.
Skapa förståelse för decimaltal
När jag möter elever i matematiksvårigheter saknar de ofta förståelse för decimaltal och motsvarigheten i bråkform samt sambandet mellan dessa. Eleverna förstår inte värdet av de olika positionerna, vilket resulterar i ett mekaniskt användande av siffrorna vid omvandlingar mellan bråk-, decimal- och procentform samt vid aritmetiska beräkningar. Löwing (2006) och Ohlsson (2013) uppmärksammar detta i sin forskning och de menar att missuppfattningar som att 0,237 är större än 0,4 är vanliga bland eleverna. Alla ni som satt er in i matematiklyftets modul om taluppfattning och tals användning känner igen diskussionen.
I min undervisning försöker jag alltid att konkretisera det matematiska innehållet för att skapa en förståelse för det som ska abstraheras. Genom olika uttrycksformer vill jag ge eleverna en så nyanserad begreppsbild som möjligt. Forskning visar att eleverna behöver handledning mellan den konkreta representationsformen, via den halvkonkreta till de abstrakta representationsformerna (Rystedt och Trygg, 2010). Tallinjen är ett viktigt verktyg för att skapa en inre visualisering av bråk- och decimalform. Dock vill jag i denna blogg tipsa om tiobassystemet som stöd vid konkretiseringen av decimalsystemet. Idén har jag fått från en artikel i Nämnaren (NCM, 2007) och även McIntosh (2008).
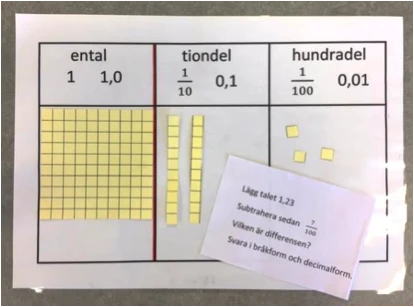
Tiobasmaterialet finns i trä eller plast i många lågstadieklassrum men för åk 4-9 fungerar det utmärkt att tillverka eget material genom att klippa ut de olika ”baserna” av centimeterrutat papper. I arbetet med materialet använder jag 100-plattan som ental, denna kan jag dela i 10 st tiondelar (ursprungsmaterialets tiotal) eller 100 hundradelar (ursprungsmaterialets ental). Det går också lätt att se att en tiondel är lika med 10 hundradelar. Genom att klippa en hundradel i tio delar illustrerar jag hur liten en tusendel är, o.s.v. Vid behov kan materialet användas tillsammans med ett positionsschema.

Konkretiseringsmodellen går att använda både i helklass och i mindre grupp. Dylan William (2013) menar att vi, genom att få alla elever aktiva under bl.a. genomgångar, kan höja måluppfyllelsen och få fler elever med på tåget. Det är därför en fördel om alla elever har tillgång till materialet samtidigt, kanske i kombination med miniwhiteboards. På så vis kan man dynamiskt röra sig mellan de olika representationsformerna ovan. Då eleverna blivit förtrogna med materialet arbetar jag först med 10-basmaterialet vid gemensamma genomgångar och därefter får eleverna göra uppgifter till varandra i grupper/par. När eleverna själva får vara kreativa kan de också påverka svårighetsnivån. Genom olika frågeställningar lägger resp. skriver eleverna talen och får möjlighet att storleksordna, addera, subtrahera, växla m.m. Stambråken och dess decimalformer (1/2= 0,5 1/4 = 0,25 ) är också lätta att undersöka och konkretisera.

Som komplement till materialet är appen Number Pieces Basic rolig att arbeta med. Den är en digital variant av 10-basmaterialet. NCM:s sträva Färglägg decimaler är ett bra komplement som ökar förståelsen ytterligare.
Fördjupning
Hilling Drath, Maria (2007). Konkretition av decimaltal.
Löwing, Madeleine (2006). Matematikundervisningens dilemman. Studentlitteratur
McIntosh (2008). Förstå och använda tal. Göteborgs univseritet, NCM, Göteborgs universitet
NCM. Färglägg decimaler.
Olsson, Ingrid (2013). Tal i decimalform.
Rystedt, Elisabeth och Trygg, Lena (2010). Laborativ matematikundervisning – vad vet vi?. NCM, Göteborgs universitet
Wiliam, Dylan (2013). Dylan Wiliam om lärandets vitala verktyg. Föreläsning tillgänglig på Internet: http://www.ur.se/Produkter/183747-Larandets-idehistoria-Dylan-Wiliam-om-larandets-vitala-verktyg. Hämtad 5 december 2016. Stockholm: UR
